八大排序

插入排序

基本思想:每一步将一个待排序的数据插入到前面已经排好序的有序序列中，直到插完所有元素为止.

先确定第一个元素暂时为有序元素,声明应该变量tmp存放第二个元素这个

创建一个循环 i,从第二个元素开始向右循环(++),在循环 i 中嵌套一个循环 j 为i-1向左循环(–),假设 i 左边的元素为有序元素, 则循环 j 需要用有序元素与右边的无序元素进行比较.

假设一个数组包含{4, 6, 8, 5, 9}, i 从第二个元素6开始,向右循环,每次循环将对应的值赋予tmp,到8为止,都不需要进行排序操作,当 i 指向5时,8>5,进入循环 j,将8赋值给5所在的下标区域,循环 j 继续循环,走到6时发现6>tmp=5,所以将6给它右边的第一个值(j+1的位置),继续执行 j 循环,直到 j = 0,4<5时,则 j+1的位置为5,跳出循环 j,接着执行循环 i,最后完成排序.

算法适用于少量数据的排序，时间复杂度为O(n^2)。是稳定的排序方法。

时间复杂度为O(n^2),

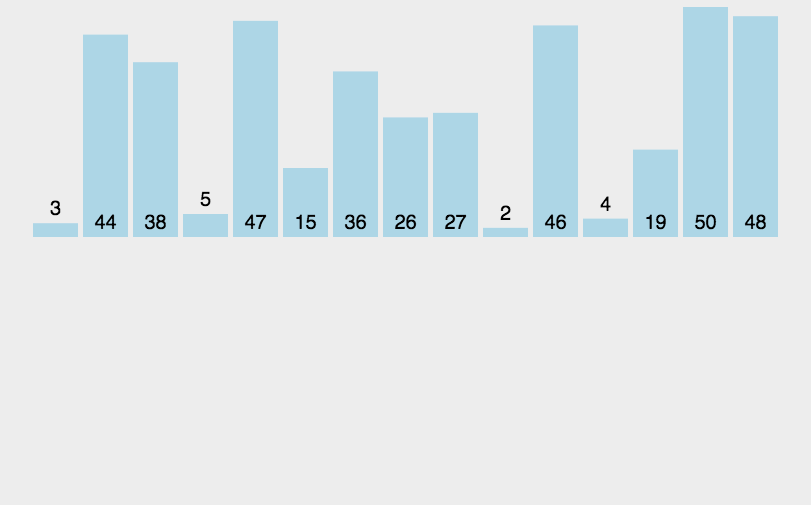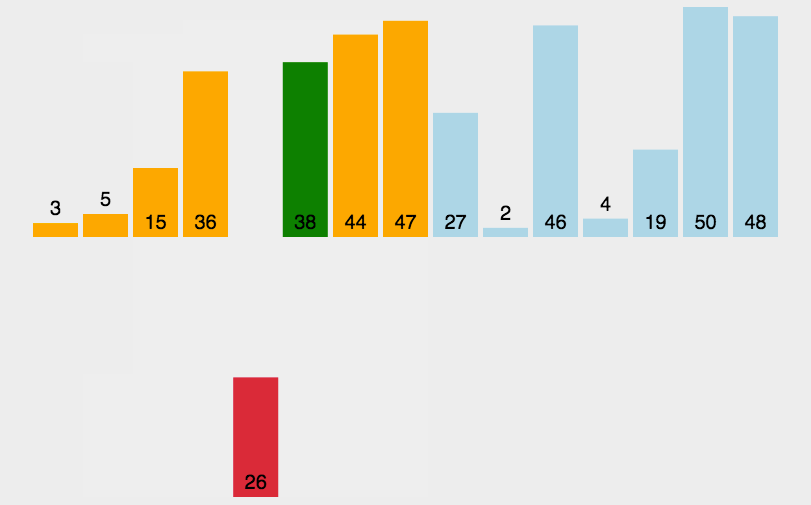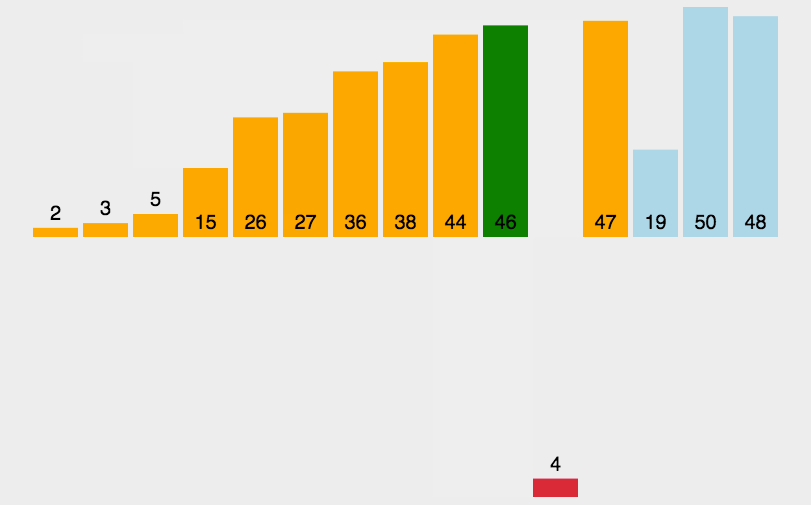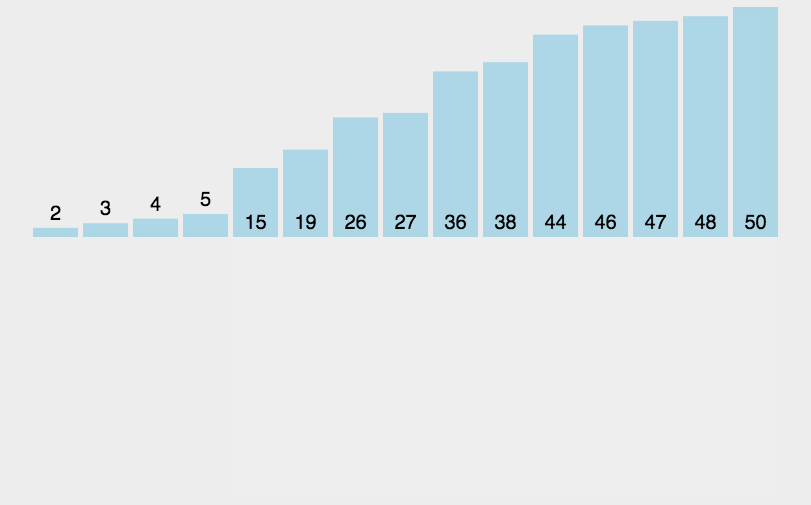
代码实现:

int[] array = new int[]{4, 6, 8, 5, 9};
int i;
int j;
//从第二个元素开始循环数组
for (i = 1; i < array.length; i++) {
    int tmp = array[i];//将元素赋予tmp

    //从i-1个元素开始循环 判断array[j]是否大于tmp 如果大于则进入循环 开始交换
    for (j = i - 1; j > 0 && array[j] > tmp; j--) {
        //向右移动 腾出左边的空间
        array[j + 1] = array[j];
    }
    //将tmp的数插入到合适的位置
    array[j + 1] = tmp;
}

冒泡排序

基本思想:冒泡排序,类似于水中冒泡,较大的数沉下去,较小的数慢慢冒出,假设从小到大,则大的往上浮,小的往下沉.说白了,就是每遍历一趟,将最大的数移动至末尾.

比较相邻两个元素,如果前一个比后一个大,则交换.

第一趟比较,第一个和第二个比较交换,然后第二个和第三个比较交换,这样下来,最大的会到最后面,接着是下一趟.

冒泡排序最好的时间复杂度为O(n)。冒泡排序的最坏时间复杂度为O(n^2)。因此冒泡排序总的平均时间复杂度为O(n^2)。

代码实现:

int[] array = new int[]{4, 6, 8, 5, 9};
for (int i = 0; i < array.length; i++) {
    for (int j = i; j < array.length; j++) {
        if (array[i] > array[j]) {
            //交换
            int tmp = array[j];
            array[j] = array[i];
            array[i] = tmp;
        }
    }
}

选择排序

基本思想:每次排序中选择最大或最小的一个元素,存放在序列的初始位置,直到全部元素完成排序.

选择排序是不稳定的排序方法。时间复杂度 O(n^2)。

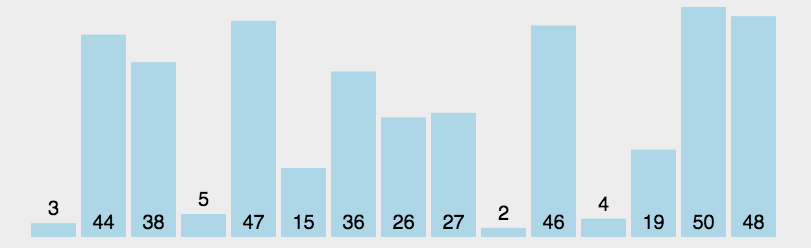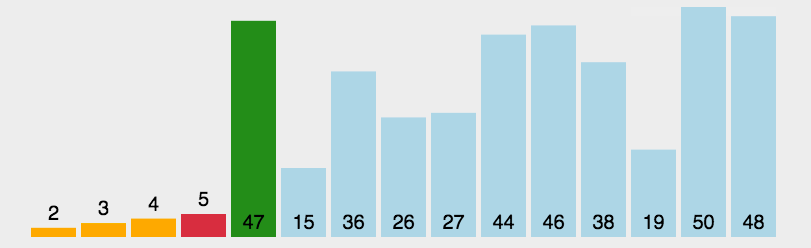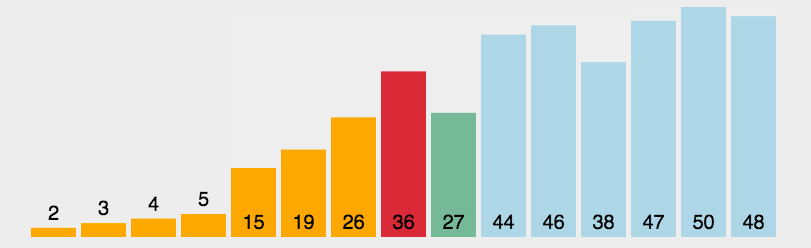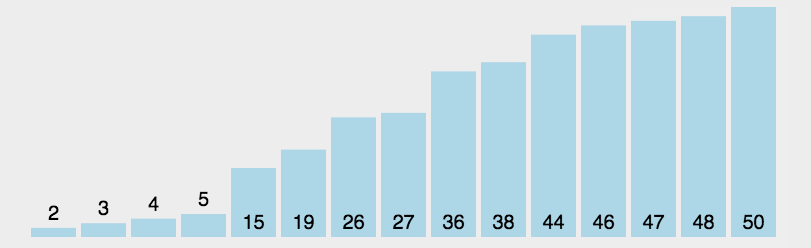
代码实现:

int[] arr = {2, 5, 4, 3, 8, 6, 4};
int sub = 0;
for (int i = 0; i < arr.length; i++) {
    sub = i;
    for (int j = i + 1; j < arr.length; j++) {
        if(arr[sub] < arr[j]){
            sub = j;
        }
    }

    if(sub != i){
        int temp = arr[sub];
        arr[sub] = arr[i];
        arr[i] = temp;
    }
}

希尔排序

基本思想:先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量dt=1(dt<dt-1…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

希尔排序不稳定，时间复杂度 平均时间 O(nlogn) 最差时间O(n^2)

int[] arr = {3, -1, 45, 98, 1, 34, 56, 0, -2, -89, 2};

//控制希尔变量
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
    for (int i = gap; i < arr.length; i++) {
        for (int j = i - gap; j >= 0; j -= gap) {
            if (arr[j] > arr[j + gap]) {
                int temp = arr[j];
                arr[j] = arr[j + gap];
                arr[j + gap] = temp;
            }
        }
    }
}

参考视频:希尔排序动画演示

堆排序

参考

插入排序/希尔排序:https://blog.csdn.net/qq_33289077/article/details/90370899

选择排序:https://www.jianshu.com/p/51100da14cc2